Круги эйлера — примеры и методы решения логических задач

Прямоугольник

Самая неустойчивая фигура психогеометрии. Ими бывают почти все дети, а также другие фигуры, когда они в стрессе. Хотя некоторые люди настолько инфантильны и зависимы от чужого мнения, что так и остаются прямоугольниками на долгие годы. Это фигура роста, определенной стадии в жизни человека. Прямоугольники многое еще не знают или не понимают, они чаще остальных задают вопросы, они любопытны и им многое интересно. Они охотно слушают различные объяснения, ходят на экскурсии, читают мнения и комментарии других людей. У них зачастую не сформировано еще собственное мнение, пэтому они охотно перенимают мнения других людей. В одежде – меняют стили в одежде, постоянно копируя кого-то. Рабочее место – может меняться, утром – порядок, к вечеру – бардак на столе. Автомобили – они покупают, четко следуя принципу «на чем ездят остальные». Зачастую они переоценивают или недооценивают собственные силы. Когда остальные фигуры по психогеометрии впадают в стрессовое состояние, они становятся неустойчивыми прямоугольниками: неопределенными, колеблющимися. Например, сильные и властные треугольники начинают пить, квадраты становятся хаотичными и неаккуратными, круги замыкаются в себе и молчат, а зигзаги сидят на кресле и смотрят в потолок или в окно, и ничего не хотят делать.

источник

Решение задач с помощью кругов Эйлера

Давайте рассмотрим несколько примеров задач, которые можно решить с помощью кругов Эйлера.

Задача про любимые мультфильмы

Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах. Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок», шестерым — «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма. У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка Боб Квадратные Штаны».

Решение:

Так как по условиям задачи у нас даны три множества, чертим три круга. А так как по ответам ребят выходит, что множества пересекаются друг с другом, чертеж будет выглядеть так:

Мы помним, что по условиям задачи среди фанатов мультфильма «Волк и теленок» пятеро ребят выбрали два мультфильма сразу:

Выходит, что:

21 – 3 – 6 – 1 = 11 – ребят выбрали только «Белоснежку и семь гномов».

13 – 3 – 1 – 2 = 7 – ребят смотрят только «Волк и теленок».

Осталось только разобраться, сколько шестиклассников двум другим вариантам предпочитает мультфильм «Губка Боб Квадратные Штаны». От всего количества учеников отнимаем всех тех, кто любит два других мультфильма или выбрал несколько вариантов:

38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только «Губка Боб Квадратные Штаны».

Теперь смело можем сложить все полученные цифры и выяснить, что:

мультфильм «Губка Боб Квадратные Штаны» выбрали 8 + 2 + 1 + 6 = 17 человек. Это и есть ответ на поставленный в задаче вопрос.

А еще давайте рассмотрим задачу, которая в 2011 году была вынесена на демонстрационный тест ЕГЭ по информатике и ИКТ (источник — http://eileracrugi.narod.ru/index/0-6).

Условия задачи:

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.

Запрос	Найдено страниц (в тысячах)
Крейсер | Линкор	7000
Крейсер	4800
Линкор	4500

Какое количество страниц (в тысячах) будет найдено по запросу Крейсер & Линкор?

Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

При помощи кругов Эйлера изобразим условия задачи. При этом цифры 1, 2 и 3 используем, чтобы обозначить полученные в итоге области.

Опираясь на условия задачи, составим уравнения:

1. Крейсер | Линкор: 1 + 2 + 3 = 7000
2. Крейсер: 1 + 2 = 4800
3. Линкор: 2 + 3 = 4500

Чтобы найти Крейсер & Линкор (обозначенный на чертеже как область 2), подставим уравнение (2) в уравнение (1) и выясним, что:

4800 + 3 = 7000, откуда получаем 3 = 2200.

Теперь этот результат мы можем подставить в уравнение (3) и выяснить, что:

2 + 2200 = 4500, откуда 2 = 2300.

Ответ: 2300 — количество страниц, найденных по запросу Крейсер & Линкор.

Как видите, круги Эйлера помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.

Психология форм

Все визуальные объекты могут быть проанализированы с точки зрения формы. Например, дом может восприниматься как прямоугольник с треугольником сверху, а солнце часто представлено как круг с линиями вокруг него. Люди не всегда могут заметить, какие фигуры и формы окружают их, но все же они оказывают большое влияние на наше сознание и поведение. Наука, изучающая влияние форм на людей, известна как психология форм.

В исследованиях утверждается, что каждая форма имеет свой собственный смысл и влияет на наш разум и реакции. Есть много психологических тестов, которые используются для определения личности или психического состояния посредством форм. Например, выбранная форма может рассказать о чертах характера человека.

Многолетние исследования и тесты помогли специалистам определить, какое значение привносит каждая форма и как она может влиять на восприятие человеком. Давайте посмотрим поближе.

Квадрат Декарта — техника принятия решений

Пользоваться техникой легко. Как сказано выше, на листе бумаги следует нарисовать квадрат. Можно просто разделить его на четыре части горизонтальной и вертикальной линией. Запишите вопросы.

Заполняйте квадрат вдумчиво. На каждый вопрос давайте 5-8 ответов. Тщательно анализируйте записи. Оценивайте плюсы и минусы каждого варианта. Только потом делайте выбор.

Как принять решение

После заполнения всех полей внимательно прочитайте записи. Отметьте плюсом все преимущества, а минусом недостатки каждого пункта. Проанализируйте, чего больше. А дальше действуйте. Если плюсов больше, принимайте решение. В противном случае взвесьте все еще раз. Потом посмотрите на ситуацию с другой стороны.

Логические задачи и круги Эйлера

Круги Эйлера – это геометрическая схема. С ее помощью можно изобразить отношения между подмножествами (понятиями), для наглядного представления.

Способ изображения понятий в виде кругов позволяет развивать воображение и логическое мышление не только детям, но и взрослым.

Начиная с 4-5 лет детям доступно решение простейших задач с кругами Эйлера, сначала с разъяснениями взрослых, а потом и самостоятельно.

Овладение методом решения задач с помощью кругов Эйлера формирует у ребенка способность анализировать, сопоставлять, обобщать и группировать свои знания для более широкого применения.

Пример

На рисунке представлено множество – все возможные игрушки. Некоторые из игрушек являются конструкторами – они выделены в отдельный овал. Это часть большого множества «игрушки» и одновременно отдельное множество (ведь конструктором может быть и «Лего», и примитивные конструкторы из кубиков для малышей). Какая-то часть большого множества «игрушки» может быть заводными игрушками. Они не конструкторы, поэтому мы рисуем для них отдельный овал. Желтый овал «заводной автомобиль» относится одновременно к множеству «игрушки» и является частью меньшего множества «заводная игрушка». Поэтому и изображается внутри обоих овалов сразу.

Вот несколько задач для маленьких детей на логическое мышление:

Определить круги, которые подходят к описанию предмета

При этом желательно обратить внимание на те качества, которыми предмет обладает постоянно и которыми временно. Например, стеклянный стакан с соком всегда остается стеклянным, но сок в нем есть не всегда

Или существует какое-то обширное определение, которое включает в себя разные понятия, подобную классификацию тоже можно изобразить с помощью кругов Эйлера. Например, виолончель – это музыкальный инструмент, но не каждый музыкальный инструмент окажется виолончелью.

Определение круга, который не подходит к описанию предмета. Например, баранка – она круглая и вкусная, а определение зеленая к ней не подходит. Можно также придумать, какой предмет подойдет для пересечения другой пары кругов. Пример – круглая и зеленая может быть пуговица.

Определить предмет, который подходит под описание всех кругов. Для каждого круга выбирается какое-либо качество (например – сладкое, оранжевое, круглое). Ребенок должен назвать предмет, который одновременно соответствует всем этим описаниям (в данном примере подойдет апельсин), также можно спросить ребенка, какие предметы могут соответствовать двум описаниям из трех, то есть будут находиться на пересечении каждой пары кругов (например, сладкое и оранжевое – карамелька, оранжевое и круглое – мяч, круглое и сладкое – арбуз).

Для детей постарше можно предлагать варианты задач с вычислениями – от достаточно простых до совсем сложных. Причем самостоятельное придумывание этих задач для детей обеспечит родителям очень хорошую разминку для ума.

1.Из 27 пятиклассников все изучают иностранные языки – английский и немецкий. 12 изучают немецкий язык, а 19 – английский. Необходимо определить, сколько пятиклассников заняты изучением двух иностранных языков; сколько не изучают немецкий; сколько не изучают английский; сколько изучают только немецкий и только английский?

При этом первый вопрос задачи намекает в целом на путь к решению этой задачи, сообщая, что некоторые школьники изучают оба языка, и в этом случае использование схемы также упрощает понимание задачи детьми.

1. источник http://shkolazhizni.ru/school/articles/71462/
2. автор Леонид Серый
3. Кстати, если вы не можете определиться, какую профессию выбрать, попробуйте нарисовать схему в виде кругов Эйлера. Возможно, чертеж вроде этого поможет вам определиться с выбором:

Те варианты, которые окажутся на пересечении всех трех кругов, и есть профессия, которая не только сможет вас прокормить, но и будет вам нравиться.

И еще одна табличка…

Примеры задач и решения

Рассмотрим задачи, в которых помогают разбираться круги Эйлера, примеры решения задач по логике и математике.

Задачи для дошкольников

Первые в очереди: круги Эйлера для дошкольников, задания с ответами на которые помогут понять, как малыши впервые знакомятся с методикой упрощения сложных математических и логических задач.

Задание №1 – начальный уровень.

Цель: научить ребенка определять предмет, наиболее соответствующий одновременно двум свойствам.

Правильный ответ: кубик Рубика.

Правильный ответ: лягушка.

Правильный ответ: груша.

Задания усложняются тем, что используется больше множеств.

Правильный ответ: Солнце.

Правильный ответ: платье.

Задание №6

Правильный ответ: полезные.

Задания для школьников

Следующие задачи по логике с ответами, круги Эйлера в которых являются основой для решения, касаются младших школьников. Подобные задания обучают детей разбирать логические пересечения по определенным признакам.

Задание №1

35 учеников зарегистрированы в школьной или городской библиотеках. Из них 25 регулярно посещают школьную библиотеку, а 20 – городскую.

Сколько учеников:

• Посещают обе библиотеки?
• Не посещают городскую библиотеку?
• Не посещают школьную библиотеку?
• Ходят только в городскую библиотеку?
• Ходят только в школьную библиотеку?

Ответ:

Определим количество посетителей двух библиотек – общая часть на диаграмме:

(25 + 20) – 35 = 10.

Ученики, не посещающие городскую библиотеку:

35 – 20 = 15 – левая сектор голубой зоны.

Ученики, не посещающие школьную библиотеку:

35 – 25 = 10 – правый сектор фиолетовой.

Посетители только городской библиотеки:

35 – 25 = 10 – также, правый сектор фиолетовой.

Посетители только школьной библиотеки:

35 – 20 = 15 – также, левый сектор голубой.

В 7-А учится 38 человек. Ученики увлекаются разными спортивными играми: 16 – баскетболом, 17 – хоккеем, 18 – футболом. Одновременно баскетбол и хоккей любят 4 человека, баскетбол и футбол – 3, хоккей и футбол – 5, а 3 ученика не интересуются спортом.

Вопрос:

1. Есть ли ученики, увлекающиеся всеми спортивными играми?
2. Какое количество школьников интересуется только одной из спортивных игр?

Ответ:

Все ученики класса – наибольшая окружность.

Круг «Б» — баскетболисты, «Х» — хоккеисты, «Ф» — футболисты, «Z» — универсальные спортсмены. Трое неспортивных учеников просто находятся в общем круге.

Баскетболисты, входящие в множество «Б», но не входящие в зоны пересечения со множествами «Х» и «Ф».

16 – (4 + Z + 3) = 9 – Z.

По аналогии, находим количество хоккеистов.

17 – (4 + Z + 5) = 8 – Z.

Футболисты.

18 – (3 + Z + 5) = 10 – Z.

Чтобы пределить значение Z, нужно суммировать множества учеников.

3 + (9 – Z) + (8 – Z) + (10 – Z) + 3 + 4 + 5 + Z = 38;

42 – 2*Z = 38;

Z = 2.

Соответственно, Б = 7, Ф = 8, Х = 6.

Применение круговых диаграмм позволяет наглядно продемонстрировать все взаимоотношения разных групп учеников.

Метод схематического изображения взаимоотношений множеств – не просто увлекательная вещь. Круги Эйлера, примеры решения задач, логика которых неочевидна, показывают, что метод может использоваться не только при развязывании математических заданий, но и находить выход из житейских ситуаций.

Как нарисовать круги эйлера в ворде

Чтобы нарисовать в программе ворд круги Эйлера, нужно воспользоваться комбинацией двух программ: Word и Paint. Рассмотрим, подробно, как можно это сделать.

Первый шаг. Открываем, пустую папку на компьютере. Нажимаем в любое место в папке, правой кнопкой мыши, чтобы появилось меню, в котором нужно выбрать «Создать», а там выбрать: «Точечный рисунок».

Второй шаг. В папке появляется новый файл, который выделяем и затем жмем на правую кнопку мыши. На экране появится меню, в котором выбираем «Открыть с помощью», появляется еще одно подменю и нажимаем на «Paint».

Третий шаг. На экране откроется программ Paint и перед нами будет белый лист. На верхней панели находим блок «Фигуры», выбираем «Овал» и рисуем два круга.

Четвертый шаг. Сделаем внутри кругов подписи: «А» и «В». Для этого на верхней панели находим блок «Инструменты» и жмем на ярлык буквы А.

Еще остается отредактировать рисунок, с помощью кнопки «Выделить» выделяем только нужную область и нажимаем на кнопку «Обрезать», чтобы убрать лишнее. Затем верхней части выбираем «сохранить как» и сохраняем в формате *.jpeg.

Пятый шаг. Открываем чистый лист программы ворд, на верхней панели настроек выбираем закладку «Вставка», там ищем блок «Иллюстрация» и нажимаем на иконку с надписью «Рисунок».

Шестой шаг. Откроется меню, где вы должны найти папку с сохраненным ранее файлом. В ней выбрать фотографию с кругами Эйлера и вставить.

Задача по рисованию кругов Эйлера в программе ворд выполнена.

Примечание: Мы стараемся как можно оперативнее обеспечивать вас актуальными справочными материалами на вашем языке. Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки

Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы

Для удобства также приводим ссылку на оригинал (на английском языке).

Вы можете создать графический элемент SmartArt, который использует макет диаграммы Венна в Excel, Outlook, PowerPoint и Word. Диаграммы Венна идеально подходят для иллюстрации сходствов и различий между различными группами или концепциями.

Общие сведения о диаграммах Венна

На диаграммах Венна можно с помощью перекрывающихся кругов продемонстрировать сходство, различия и связи между понятиями, идеями, категориями или группами. Сходство между группами представлено перекрывающимися частями кругов, а различия — неперекрывающимся.

1. Каждая крупная группа представляется одним из кругов.

2. Каждая область перекрытия соответствует сходству между двумя большими группами или входящими в них более мелкими.

В программе Microsoft Word огромное количество готовых автофигур, макетов, диаграмм и других полезных инструментов для представления интересной информации и сравнения данных. А такая геометрическая фигура, как круг встречается часто в математических работах, в расчетных графиках, в творческих иллюстрациях. В данной статье рассмотрим, как в ворде нарисовать круг.

Круги Эйлера и примеры задач на логику

На самом деле, круги Эйлера очень часто встречаются в нашей жизни. Уже в начальной школе ученики начинают работать со схематическими диаграммами, которые наглядно объясняют взаимосвязь между объектами и понятиями.

Эйлеровы круги — это геометрические структуры, используемые для упрощения распознавания рациональных отношений между объектами, понятиями и явлениями.

В зависимости от типа отношений между множествами, они делятся на группы.

• равнозначные (рис.1);
• пересекающиеся (рис.2);
• подчиненные (рис.3);
• соподчиненные (рис.4);
• противоречащие (рис.5);
• противоположные (рис.6).

Типичные примеры таких диаграмм:.

Самый большой зеленый набор представляет все вариации игры.

Одним из вариантов игры является производитель. Он отмечен синим овалом. Мейкер — это независимый набор и в то же время часть всей «игры».

Игры с часами также являются частью набора «Игры», но не являются частью общего набора «Создатель». Поэтому они отмечены фиолетовым овалом. Набор «курдские автомобили», с другой стороны, является независимым набором, но подмножеством набора «курдские игры».

Используя этот метод, ученые решали самые сложные математические задачи. Используя простые формы, они смогли свести любое решение к символической логике, то есть к максимальной простоте рассуждений, даже для самых сложных задач.

Затем метод был доработан Джоном Бенном в Великобритании, который ввел понятие множества наборов пересечений.

Методология очень проста в использовании — эйлеровский цикл уже преподается в детских садах для 4-5-летних детей. Однако он также достаточно прост для использования в высшей академической среде.

Значение размера

Размеры отдельных форм, общей композиции указывают на самооценку. Расшифровка:

1. Рисунки, которые занимают все свободное место на листе, указывают на то, что личность не может добиться чего-либо в жизни, старается компенсировать это изображением. Чаще это люди-экстраверты, которые не могут по достоинству реализовать себя в своих начинаниях.
2. Большие рисунки — обозначают высокую самооценку. Очень крупные фигуры, могут говорить о том, что субъекту присуща излишняя гордость, тщеславие, высокомерие. Глубинная причина проявления этих чувств — неудовлетворенность привычной жизнью.
3. Большое количество пустого пространства на листе присуще интровертам. Такие люди скованны, зажаты в себе, боятся чего-то нового. Они не доверяют окружающим, бояться совершать ошибки.

Психология форм в дизайне UX — значение естественных форм

Все вещи, созданные природой, имеют свою уникальную форму. Источником вдохновения для художников и дизайнеров становятся листья, цветы, деревья, животные и многие другие представители флоры и фауны. Природные формы имеют четкие значения растений и животных, которых они символизируют. Они часто приносят ощущение освежения и единства с окружающей средой. Кроме того, животные и растения могут также иметь свои собственные характеристики и символы. Например, роза — это цветок любви и страсти, а лев — символ гордости и храбрости.

Общие значения:

• оригинальность;
• органичность;
• баланс;
• отдых.

Принцип кругов Эйлера

Вспомните эмблему CHARMED. Она нужна для визуализации.

Эйлеровский мир в реальной жизни.

На самом деле все настолько просто, что лучший и самый простой из эйлеровых методов называется «три круга». Чтобы использовать эту простую технику, вам понадобятся три разных цветных карандаша и бумага. Честность, а не обман, интеллект ума! Вы научитесь мыслить еще более рационально, чем когда-либо прежде!

Помните об инструменте «Круг А». Например, «Что я хочу делать?»., «Что я делаю хорошо?»., «Как я могу получить прибыль или доход от этого?». .

Именно здесь необходима удачная серия эмблем. Нарисуйте три круга (каждый круг — другого цвета) так, чтобы круги пересекались и образовывали внутри себя клевер.

Назовите круги на носителе, дав каждому кругу свое имя

Полностью объясните важность каждого инструмента. Что вам в нем нравится? Напишите, почему вам это нравится

Напишите, сколько вы хотите выиграть, и укажите причину — поставьте цель. Напишите, почему вы делаете что-то лучше, чем другие, отдайте себе должное.

Очень важно разрабатывать круг до тех пор, пока не сформируется клевер. Да, круги могут не пересекаться

Затем вам нужно подумать о том, как их наложить друг на друга. Возможно, потребуется замена инструментов. Круги могут иметь разные размеры. Внутренние числа не обязательно должны иметь равные части. Самое главное — иметь эти детали.

Спроектировав круг и распределив работу, в центре появляется фигура, напоминающая треугольник. Эта форма является основным отношением «подмножества» и дает конечный результат. Получившаяся листовка — это путь к конечному результату.

Колесо жизненного баланса

Жизнь человека разнообразна и наполнена множеством интересов и занятий. Но если хорошенько подумать, то все «содержимое» нашего существования можно условно разделить на несколько областей, в которых мы неизбежно будем задействованы.

Очень важно, чтобы эти области находились в гармонии между собой, сохраняли баланс. Если какая-то сфера жизни начинает отставать в развитии или, напротив, опережать остальные, то возникает дисбаланс

Таким образом появляются проблемы разного характера.

Например, человек очень увлечен построением карьеры и все свое время и силы посвящает этому занятию

Конечно, у него образуется пустота в личной жизни, так как не остается времени, чтобы уделить внимание родным, близким, друзьям, детям

Заняться вопросами здоровья также получается не всегда вовремя. Постепенно это приводит к целому набору нерешенных проблем.

Не страшно, если такая ситуация возникает на время. Например, если нужно срочно довести до конца какой-то важный проект. Он на протяжении определенного периода занимает большую часть времени, но с его окончанием все должно вернуться в нормальное русло. Плохо, если так происходит постоянно, систематически.

Для того чтобы понять, почему именно произошла разбалансировка, а также разобраться в том, как привести все в порядок, когда-то был придуман интересный психологический инструмент – колесо жизненного баланса (колесо жизни). Идею его создания приписывают некоему Полу Джону Мейеру. Одни источники утверждают, что он был терапевтом, в других его именуют психологом, а где-то говорится, что Мейер специализировался на коучинге. Но это не самая важная информация. Главное, что придуманный им инструмент и одноименное упражнение реально работают. И в настоящее время они очень востребованы в области саморазвития и личностного роста.

Если научиться правильно использовать колесо баланса, то можно увидеть, откуда берутся неприятности, проанализировать и дать оценку каждой сфере своей жизни, верно расставить между ними приоритеты, поставить цели и наметить пути их достижения. С помощью колеса жизни возможно выявить сильные стороны личности, а также слабые, требующие большего внимания, дополнительного развития и корректировки.

Данный метод очень прост. Для его освоения не надо специальной подготовки. Главное, быть честным с самим собой и, предварительно подумав, давать правдивые ответы на вопросы. Таким образом, картина жизни будет прорисована без прикрас, объективно. И станет ясно, в каком направлении надо двигаться.

Примеры применения

Проблема Кенигсбергского моста

Проблема моста Кёнигсберга может быть выражена в следующем графике:

График для задачи о Кенигсбергском мосту

Круги ( узлы ) — это соответствующие районы города или точки обзора. Линии ( ребра ) — это мосты. Методом проб и ошибок установлено, что невозможно найти экскурсию по городу, в которой каждый мост использовался бы ровно один раз. Таким образом, нет пути Эйлера и, следовательно, нет круга Эйлера. Почему это так?

Эйлер открыл следующий закон: если в графе G есть путь Эйлера, то нечетные степени имеют максимум 2 узла. В графе Кенигсбергского моста четыре узла с нечетными степенями. Цифры рядом с узлами указывают их степени на иллюстрации. Поэтому экскурсия по городу с одним использованием каждого моста невозможна.

Нечетный узел — это либо начало, либо конец пути по мостам: ноль нечетных узлов будет означать, что начало и конец пути в Кенигсберге идентичны. Путь с началом и концом будет иметь максимум два нечетных узла. Следовательно, в Кенигсберге нельзя было пересечь все мосты в одну сторону только один раз.

Дом Святого Николая

→ Основная статья : Дом Николая

Популярная детская головоломка «Это дом Святого Николая», напротив, содержит путь Эйлера, но не круг Эйлера, так как его граф содержит два узла степени 3.

Такой путь Эйлера — 1-2-4-3-1-4-5-3-2. Узлы 1 и 2 имеют по 3 соседа, поэтому их степень нечетная . Чтобы нарисовать дом за один раз, вам нужно начать с одной из этих двух точек. Квадрат с диагоналями не содержит пути Эйлера, так как все его узлы имеют степень 3. На рисунке это только точки 1, 2, 3, 4 со стыковочными краями.

Конспект и презентация к уроку по информатике «Круги Эйлера»

• Тип урока: интегрированный с математикой, урок обобщения и систематизации знаний, умений и навыков.
• Вид урока: урок теоретических и практических работ, анализ ситуации.
• Методы обучения: диалогический, наглядный, объяснительно – иллюстративный.
• Формы обучения: коллективная и индивидуальная.

Структура урока: орг.

момент, актуализация опорных знаний, формирование новых понятий и способов действий, систематизация ЗУН, закрепление полученных навыков и умений, самостоятельная работа, подготовка к восприятию Д/З, подведение итогов урока.

1. Цели урока:
2. обобщить знания и умения обучающихся по применению таблиц истинности при решении логических задач;
3. познакомить и сформировать у обучающихся принцип реализации диаграмм Вена — Эйлера для решения логических задач;
4. развить коммуникативно — технические умения, умения оценивать результаты выполненных действий;
5. развить аналитическо — логическое мышление;
6. воспитать самостоятельность, инициативность, толерантность, ответственное отношение к информации, информационную культуру.
7. Задачи урока:
8. повторить изученный материал по теме «Логика»;
9. научить обучающихся использовать круги Эйлера при решении логических задач;
10. продемонстрировать решение типовых задач из ГИА и ЕГЭ;
11. закрепить изученный материал решением подобных задач.

Круги Эйлера

Эйлеровы круги (круги Эйлера) — принятый в логике способ моделирования, наглядного изображения отношений между объемами понятий с помощью кругов, предложенный знаменитым математиком Л. Эйлером (1707–1783).

Он говорил о названных его именем схемах: «круги подходят для того, чтобы облегчить наши размышления». Эйлер считается немецким, швейцарским и даже российским математиком, механиком и физиком.

Дело в том, что он много лет проработал в Петербургской академии наук и внес существенный вклад в развитие российской науки.

До него подобным принципом при построении своих умозаключений руководствовался немецкий математик и философ Готфрид Лейбниц.

Метод Эйлера получил заслуженное признание и популярность. И после него немало ученых использовали его в своей работе, а также видоизменяли на свой лад. Например, чешский математик Бернард Больцано использовал тот же метод, но с прямоугольными схемами.

Свою лепту внес также немецкий математике Эрнест Шредер. Но главные заслуги принадлежат англичанину Джону Венну. Он был специалистом в логике и издал книгу «Символическая логика», в которой подробно изложил свой вариант метода (использовал преимущественно изображения пересечений множеств).

Обозначение отношений между объемами понятий посредством кругов было применено еще представителем афинской неоплатоновской школы — Филопоном (VI в. ), написавшим комментарии на «Первую Аналитику» Аристотеля.

Диаграммы Эйлера своим наглядным графическим изображением не только облегчают запоминание структуры различных сочетаний мыслей, но и помогают решению ряда задач, стоящих перед формальной логикой.

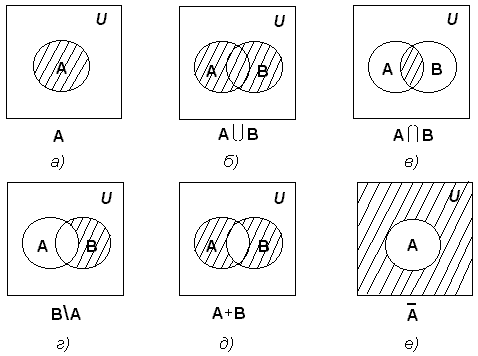
Для наглядной геометрической иллюстрации объемов понятий и соотношений между ними используется диаграммы Эйлера — Венна (круги Эйлера). Если имеются какие — либо понятия А, В, С и т. д. , то объем каждого понятия (множество) можно представить в виде круга, а отношения между этими объектами (множествами) – в виде пересекающихся кругов.

Заштрихованные области показывают результат логических операций подписанных снизу.

Весь материал – смотрите архив.

Квадрат

Главная черта характера тех, кто выбрал квадрат – трудолюбие в сочетании с организованностью, упорством, терпением и твердостью, а также пунктуальностью, чистоплотностью и практичностью. Выбор квадрата в качестве основной фигуры может свидетельствовать о склонности к аналитическому мышлению и рациональности. Такой человек все свои дела стремится сделать максимально хорошо и эффективно. А поскольку умеет управлять собой и организовывать других, то может занимать руководящие должности.

Человек-квадрат отличается консерватизмом, строгим соблюдением правил и норм, и отсутствием спонтанности и креативности. Стремится упорядочить и систематизировать все вокруг себя – пространство, вещи, любую информацию, с которой работает. Ему нравится, когда информация подается в соответствии с жесткой логикой. Выбравший квадрат человек любит, чтобы речь изобиловала фактами, цифрами и тезисами, желательно, со ссылками на источник, из которых взята. Предпочитает порядок, распланированную жизнь. Разборчив в знакомствах, не любит шумных вечеринок. В конфликтах часто уходит от прямого столкновения. Это хороший администратор и исполнитель. Проигрывает в оперативности действий, контактности с разными лицами.

Женщины, выбравшие квадрат, организованны, пунктуальны, придирчивы, внимательны к деталям. Они терпеливы, трудолюбивы, настойчивы в достижении цели, тверды в решениях и склонны к строгому соблюдению правил и инструкций. Не любят выделяться.

Люди-квадраты говорят, как правило, тихо, предпочитая не повышать голос без надобности. И не терпят повышенных тонов и у других. При этом их речь отличается ясностью, точностью, логичностью и обстоятельностью. Она бывает, как правило, несколько монотонной, «механической». Для них характерно употребление речевых штампов.

Педантичность, скрупулезность и последовательность проявляются и в выборе одежды. Эти люди предпочитают строгий, классический стиль, сдержанные, неяркие тона. Они опрятны, сухощавы. Нежелание выделяться проявляется и в жестах, которые скупы и невыразительны.